Bei einer nicht sicher vorhersagbaren Zukunft ist jedes Unternehmen Chancen und Risiken ausgesetzt, die zu Planabweichungen führen können. Die menschliche Neigung zu kognitiven Verzerrungen (Bias), also Chancen zu überbewerten und das Eintreten von Gefahren zu ignorieren („Wird schon gutgehen!“). Spätestens die Finanzkriese 2008/2009, aber noch mehr die Covid19-Pandemeie, Problem in der Lieferkette, der Ukrainekrieg und andere plötzlich eintretende Ereignisse zeigt, das viele Unternehmen grundsätzlich auf „Störungen“ des Geschäftsmodells nicht vorbereitet sind. Die Fähigkeit im Umgang mit solchen Risiken wird immer mehr zu einem Erfolgsfaktor der Unternehmensführung. Dabei können mathematische Verfahren helfen! Eines davon ist die Monte-Carlo-Simulation:
Nach einer qualitativen Risikobewertung müssen diese bewertet werden. Dazu werden die Risiken mit einer einer Verteilungsfunktion beschrieben. Dann wird mittels der Verteilungsfunktion und Zufallsexperimenten das Eintreten von Risiken simuliert.
Eine Monte-Carlo-Simulation ist solch ein mathematisches Verfahren, das in der Stochastik und Wahrscheinlichkeitstheorie verwendet wird. Hierbei werden Tausende von Zufallsexperimenten mit zufälligen Eingangsdaten durchgeführt. Jedes dieser Experimente erzeugt unterschiedliche Zufallsvariablen basierend auf Wahrscheinlichkeitsfunktionen. So kann die Eintrittswahrscheinlichkeit eines Risikos simuliert werden.
Was heißt das genau?
Wie funktioniert die Monte-Carl-Simulation?
Grundlage für die Monte-Carlo-Simulation ist das Gesetz der großen Zahlen. Es besagt, dass die relative Verteilung von Zufallsergebnissen sich umso mehr der theoretischen Wahrscheinlichkeit annähert, je häufiger der Prozess unter denselben Bedingungen wiederholt wird.
Wenn man für ein Zufallsexperiment die Münze nur 10 Mal wirft, kann das Ergebnis, in diesem Fall das Verhältnis von Kopf zu Zahl (relative Häufigkeit) von dem erwarteten 50/50-Verhältnis abweichen. Wenn man die Münze 20.000 Mal wirft, sind die Chancen größer , dass sich die relative Häufigkeit dem Wert 50/50 annähert, das das Verhältnis Kopf zu Zahl jeweils etwa 10.000 Mal auftritt. Damit gäbe es aggregiert eine Wahrscheinlichkeit von 50% für Zahl oder Kopf.
Um solche Risikosimulationen durchführen zu können, bei denen es nicht darum geht, ob Ereignis A oder B eintritt, sondern eher darum, wie sich Ereignis A z.B. auf Umsatz, Kosten und Ergebnis auswirkt, müssen vier Schritte durchlaufen werden:
1. Übergangsgleichung ermitteln
Zum Erstellen einer Monte-Carlo-Simulation wird ein quantitatives Modell des Geschäftsvorgangs, Plans oder Prozesses benötigt, der untersucht werden soll. Die mathematische Darstellung des Prozesses wird als Übergangsgleichung bezeichnet. Das wäre hier eine Gleichung Ergebnis = Umsatz – Kosten. Die Wirkungen von Einzelrisiken müssen in einem Unternehmensmodell abgebildet und hinsichtlich ihres Einflusses auf die entsprechenden Positionen, hier Umsatz und Kosten abgebildet werden.
2. Eingabeparameter ermitteln
Um eine aussagekräftige Monte-Carlo-Simulation durchzuführen zu können, ist es notwendig alle relevanten Risiken zu quantifizieren und mit Hilfe geeigneter Wahrscheinlichkeitsverteilungen zu beschreiben. Bestimmen Sie für jeden Faktor in der Übergangsgleichung die Datenverteilung, mit welcher Wahrscheinlichkeit ein Ereignis auftreten kann.
- Für das Beispiel Münzwurf wäre das eine Binomialverteilung.
- Trifft man die Annahme, dass Umsatz und Kosten bei jeder Simulation mit einem beliebigen Wert auftreten können, sich also Werte auch wiederholen könnten, so würden man eine Gleichverteilung verwenden.
- Trifft man die Annahme , dass Umsatz und Kosten in Intervallen auftreten könnten und würde das zusätzlich mit Szenarien beschreiben (best, worst, real) , dann müsste man die sogenannte Dreiecksverteilung heranziehen.
- …….
3. Simulation durchführen
Für ein aussagekräftiges Ergebnis muss ein großer Satz von Zufallszahlen für jeden Eingabeparameter erstellt werden, ungefähr in der Größenordnung von 100.000 Werten. Diese zufälligen Datenpunkte simulieren die Werte, die über einen langen Zeitraum bei den einzelnen Eingaben auftreten könnten.
4. Simulationsergebnisse analysieren
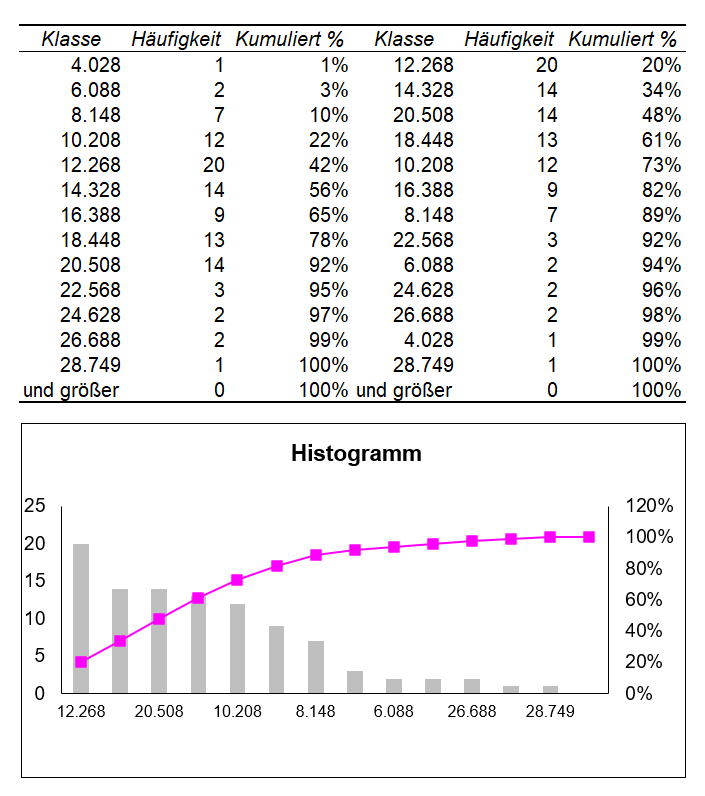
Wenn die simulierten Daten vorliegen, können Sie mit Hilfe der Übergangsgleichung simulierte Ergebnisse berechnen. Um bei dem sehr vereinfachten Beispiel zu bleiben, würde hier 100.000 mal ein Wert für Umsatz und einer für die Kosten simuliert werden und damit 100.000 mal ein Ergebnis berechnet. Mittels einer kumulierten Häufigkeitsverteilung („Bandbreitenplanung“) wird dann errechnet, wie oft ein Ergebnis im Intervall von x bis y aufgetreten ist und daraus eine kumulierte Wahrscheinlichkeit errechnet. So können Erwartungswerte des Ergebnisses sowie der zugehörige Value at Risk (VaR) als ein realistischer Höchstschaden, der mit beispielsweise 95%iger oder 99%iger Wahrscheinlichkeit nicht überschritten wird, abgeleitet werden Hinzu kommen noch die Bildung von Mittelwerten (Verteilungen) der gemessenen Größe und der statistischen Fehler, da es sich im Grunde um eine Stichprobenziehung handelt.
Umsetzung mit Excel?
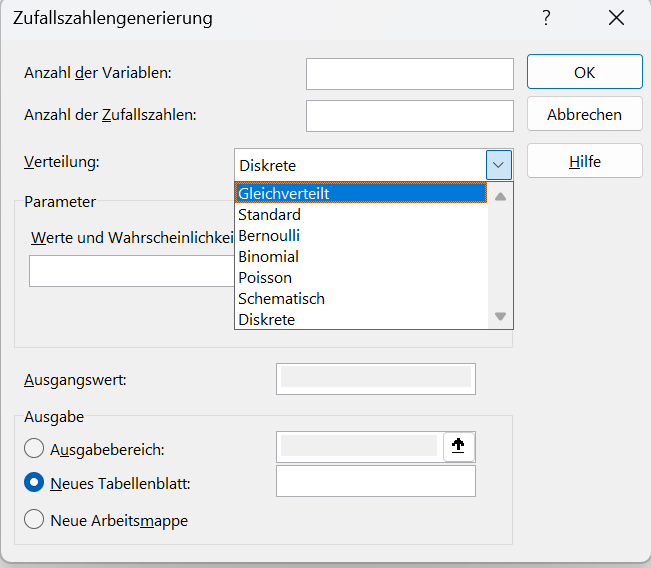
Das Durchführen einer Monte-Carlo-Simulation ist grundsätzlich mit Excel möglich, wenn die Zufallszahlengenerierung (Analyse-Add-In) eine passende Verteilungsfunktion anbietet.
Zusätzlich gibt es kaufbare Add-Ins, die eine Monte-Carlo-Simulation mit weiteren Verteilungsfunktionen ermöglichen:
- @RISK bietet eine breite Palette von Verteilungsfunktionen, Analysewerkzeugen und Visualisierungsoptionen.
- Crystal Ball ermöglicht Benutzern, Risiken in ihren Excel-Modellen zu modellieren und zu analysieren.
- ModelRisk bietet Funktionen für die Erstellung und Analyse von Monte-Carlo-Simulationen in Excel. Es umfasst verschiedene Verteilungsfunktionen und Analysetools.
- SimulAr ist ein kostenloses Add-In für Excel, das Monte-Carlo-Simulationen unterstützt. Den Anbieter scheint es nicht mehr zu geben
- Der Risk Solver ist ein Tool für die Risikoanalyse und Optimierung in Excel. Er umfasst Monte-Carlo-Simulation sowie andere fortschrittliche Analysefunktionen. Der Anbieter stellt auch das in Excel integrierte AddIn Solver zur Verfügung.
.